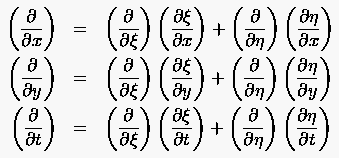Kettenregel Partielle Ableitung

In diesem kapitel schauen wir uns die kettenregel etwas genauer an.
Kettenregel partielle ableitung. Find more mathematics widgets in wolfram alpha. Wie hier zu sehen bleibt in der klammer wie gesagt die innere funktion stehen. Der wert von φ am momentanen ort r t des teilchens ist eine reine funktion f t der zeit t φ x y t r r t φ x t y t t. Ableiten mithilfe der kettenregel wann musst du die kettenregel nutzen.
Kettenregelfu r partielle ableitungen gegeben sei die bewegungsfunktion eines teilchens in der xy ebene r t x t y t 296 und ein zeitlich variierendes skalarfeld φ x y t. Viele schüler haben zu beginn größere schwierigkeiten diese regel anzuwenden. In diesem fall wäre das. Bei der kettenregel handelt es sich um eine ableitungsregel die immer dann anzuwenden ist wenn zwei funktionen miteinander verkettet ineinander verschachtelt sind.
Funktionen differenzierbar ist und gibt an wie sich die ableitung dieser abbildung berechnet. Im obigen beispiel gibt es zwei partielle ableitung weil man ja sowohl nach x als auch nach y ableiten kann. Dabei wurden die potenzregel und die faktorregel angewandt. Möchtest du nun die ableitung der funktion berechnen musst du zunächst die innere und äußere ableitung und bestimmen.
Die jeweils andere variable die nach der nicht abgeleitet wird verhält sich dabei wie eine konstante. Dafür musst du das in durch die funktion austauschen und erhältst. Sie besagt dass die verkettung von total differenzierbaren abbildungen bzw. Partielle ableitung kettenregel beweis matheloung.
Die mehrdimensionale kettenregel oder verallgemeinerte kettenregel ist in der mehrdimensionalen analysis eine verallgemeinerung der kettenregel von funktionen einer variablen auf funktionen und abbildungen mehrerer variablen. Jetzt setzt du die ableitungen und sowie die funktion in die formel für die kettenregel von oben ein. Die ableitung einer zusammengesetzten verketteten funktion erhält man als produkt aus äußerer und innerer ableitung.