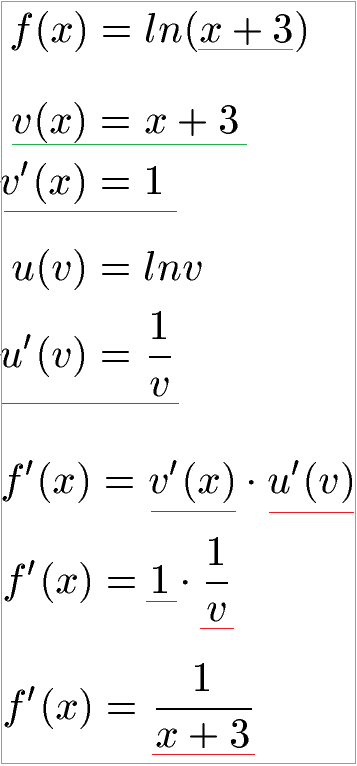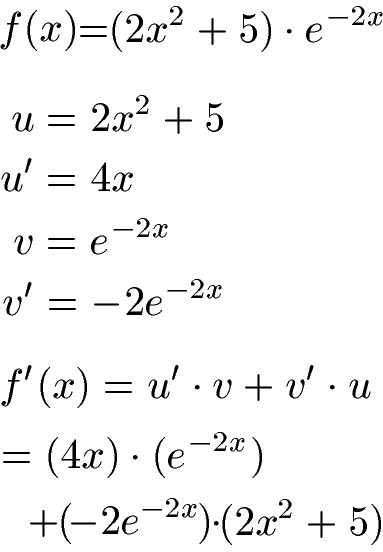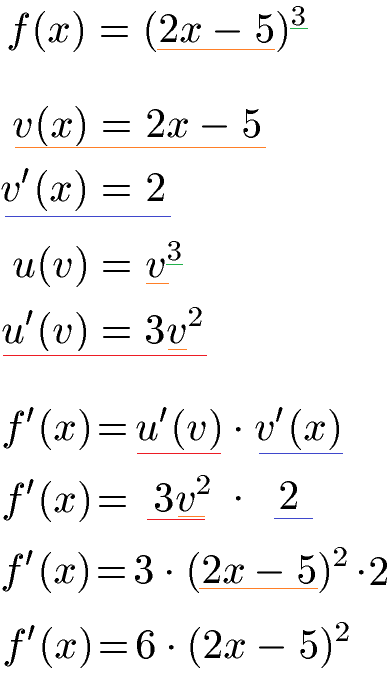Kettenregel Ableitung Mehrere Variablen
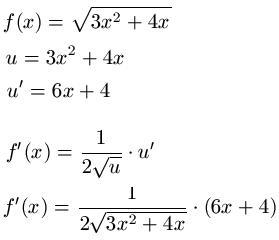
Gefragt 28 jun von ximlost.
Kettenregel ableitung mehrere variablen. Kettenregel für funktionen mehrerer variablen. Die mehrdimensionale kettenregel oder verallgemeinerte kettenregel ist in der mehrdimensionalen analysis eine verallgemeinerung der kettenregel von funktionen einer variablen auf funktionen und abbildungen mehrerer variablen. Du kannst auch deine lösungen überprüfen. F x y 2x y und nach einer der variablen abgeleitet wird spricht man von der partiellen ableitung.
Wenn eine funktion mehrere variablen hat z b. Die kettenregel mittelwertsatz und schrankensatz hoheren ableitungen und dem satz von schwarz taylor formel und lokalen extremwerten. Manchmal tritt der fall auf dass x und y nicht unabhängige variablen. Funktion 1 daumen.
Differentialrechnung in mehreren variablen. Funktionen in mehreren variablen. Z x y x e t y e t gefragt 30 nov 2015 von gast. Problematisch wird es jedoch wenn zusammengesetzte oder gar verschachtelte funktionen abgeleitet werden müssen.
Auf die jacobimatrix jg f x jg y jf x 44. In diesem kapitel schauen wir uns die kettenregel etwas genauer an. Partielle ableitung kettenregel mehrdimensionale analysis. Die verket tungseigenschaft ubertr agt sich auf das di erential.
Der ableitungsrechner kann die erste zweite fünfte ableitung berechnen. Kettenregel einsetzen mit den bisherigen ableitungsregeln ist es möglich einfache funktionen abzuleiten. Wenn eine funktion mehrere variablen hat z b. F x y 24x 20y und nach einer der variablen abgeleitet wird spricht man von der.
Ableitungen von funktionen mit mehreren variablen partielle ableitungen implizite ableitungen sowie die berechnung von nullstellen sind kein problem. Daraus folgt die totale ableitung von z nach u die durch das symbol f u. Unsere neue auffassung der ableitung zu grunde so sind die linearen funktion 1 2. Funktionen mit mehreren variablen verknüpfen untersuchen und ableiten.
Interaktive funktionsgraphen erleichtern das verständnis. Sie besagt dass die verkettung von differenzierbaren abbildungen bzw. Sei z f x y eine funktion zweier variablen x und y. Ist f ur die funktion h g f sowohl f im punkt x als auch gim punkt y f x total di e renzierbar so ist auch hin x total di erenzierbar.
Dh x dg y df x bzw. Bei der kettenregel handelt es sich um eine ableitungsregel die immer dann anzuwenden ist wenn zwei funktionen miteinander verkettet ineinander verschachtelt sind.